• 定理
• DFA 到正则表达式
  • 终止状态集的处理
  • 例子
• 正则表达式到 NFA
  • 例子
• NFA 到 DFA
  • 自动机等价和确定化
  • NFA 的确定化之子集法构造思想
    • 无ε空边 NFA 转换为 DFA—子集法
    • 带ε空边 NFA 转换为 DFA—子集法
      • 定义 1：状态集 I 的ε闭包
      • 定义 2：状态集 I 的 a 转换（状态集 I 经过输入 a 的转换状态集合）
      • 算法
      • 例子
• 参考资料

定理

对任一确定有限自动机 A，存在一正则表达式 e,使得 L(A)=L(e),反之亦然。

DFA 到正则表达式

现在有一个 DFA，要构造正则表达式，我们就给出几种构造的规则。

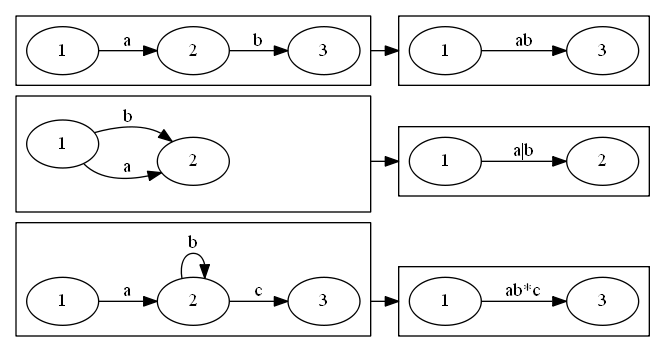
如图所示可以构造出三种规则：

• 各节点连接在一起，这个跟我们认识的结果是一样的。我们接受的就是 a 和 b 的连接相当于说接受 ab 到 3 状态
• 第二种也很好理解，走上面的路和走下面的路都行，能接受的串就是 a 或 b，正则表达式也是并的关系，解释出来相同
• 第三种就是 a 必须有 b 可以有 0~无穷 c 必须有

在自动机中的边大概就是这几种，我们可以反反复复的用这几种规则

但是实际情况 DFA 转化到正则还是有一些问题的，只有结构化的自动机¹才能转化为正则表达式。非结构化的自动机必须先转化为结构化的才能继续，转化方法有如下两个：

• 语句前加标号
• 解方程

终止状态集的处理

当出现多个终止节点时，我们可以通过将这些终止节点都连接到一个同一个虚拟的终止节点。

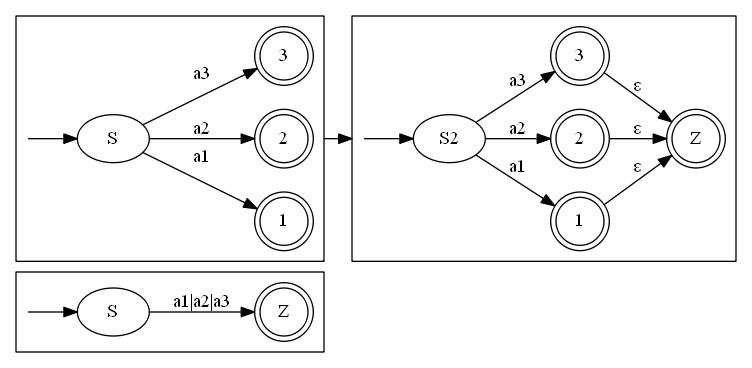
例子

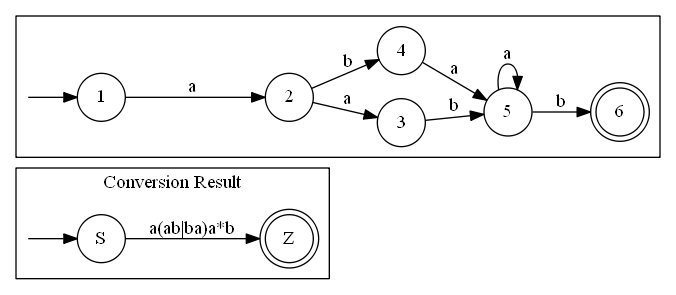
正则表达式到 NFA

Thompson 结构

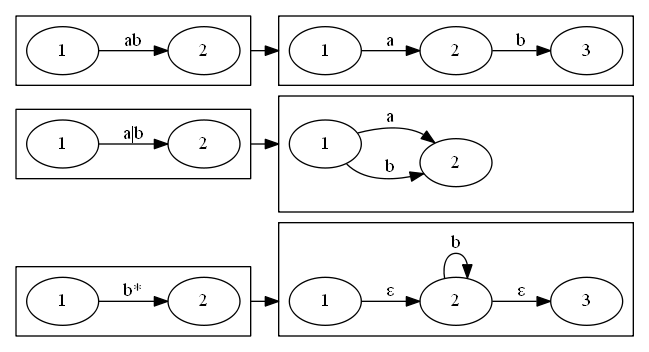
我们注意到第三张图有两个空边，我们可能会想能不能省略掉最后那个空边呢？

答案是不行的，因为在某些情况下可能会有错误。

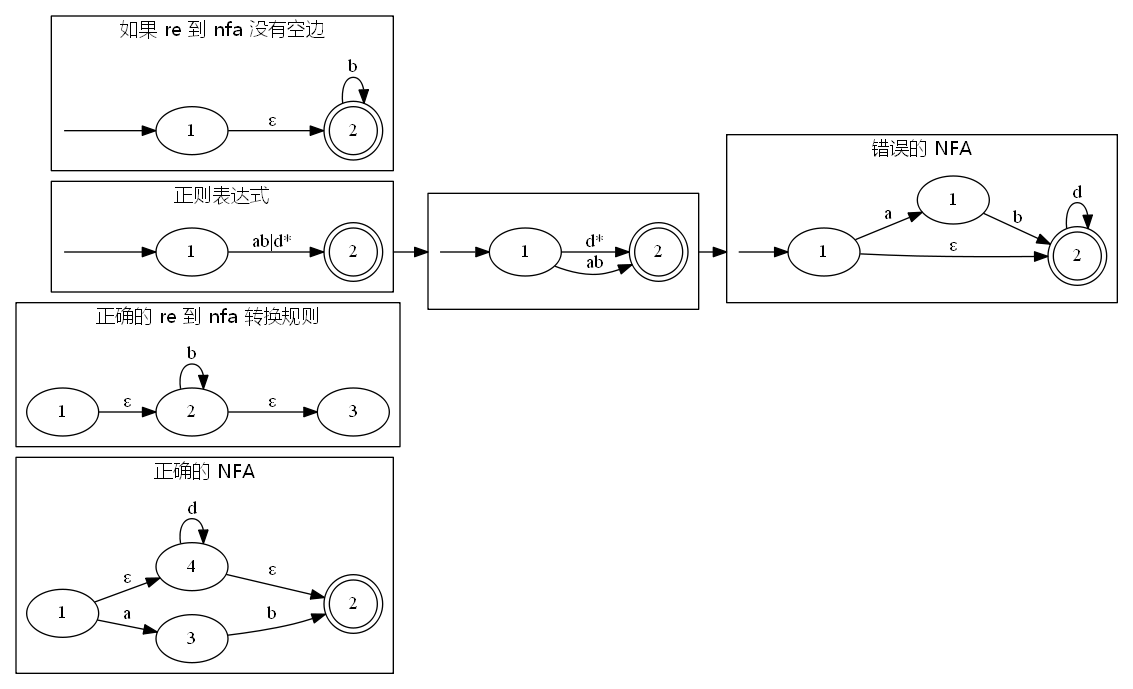
本来 ab 后面不能接 d，但是这么画完，可能就接 d 了。所以最后要有空边。

这就是我们给出的从正则表达式到自动机的规则，因为正则表达式的运算就是这么几种，我们重复使用这些规则以后，就把每一个边上都拆成了某一个字符，就变成了所谓的自动机

例子

给出一个正则表达式 (a|b)(c|d)\*(e|f) , 将其转化为 NFA

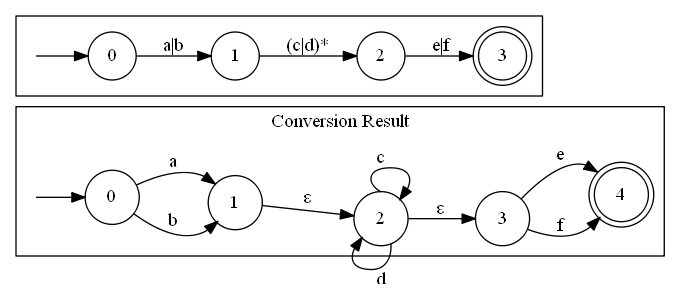
NFA 到 DFA

自动机等价和确定化

定义：设 A1 和 A2 是同一个字母表上的自动机，如果有 L(A1)=L(A2)，则称 A1 和 A2 等价

定理：对于每一个非确定有限自动机 A，存在一个确定有限自动机 A’，使得 L(A)=L(A’)

NFA 的确定化：由 NFA 构造出与其等价的 DFA 称为 NFA 确定化

NFA 的确定化之子集法构造思想

基本思想：对于 NFA 来说，开始状态是一个集合，映射到的也是一个集合，所以我们的基本思想就是把状态集看成一个状态。对于映射函数来说，左边本来是一个状态的映射，现在我们来把他也看作是一个集合，就是这个集合在接收某个符号的时候映射到某一个状态集上。按照这种思路做下去，由于 S 是有限的，所以他的幂集（子集）也是有限的，做到某个时候就会收敛

长话短说：让 DFA 的某一个状态去记录 NFA 读入一个输入符号后可能达到的一组状态

无ε空边 NFA 转换为 DFA—子集法

道理和带空边的 NFA 基本一样

带ε空边 NFA 转换为 DFA—子集法

从严格意义上来说自动机描述中是不带空边的，是为了描述的方便引入的。带空边的 NFA 的是一种比较特殊的 NFA

定义 1：状态集 I 的ε闭包

设 I 是 NFA M 状态集的子集，定义 I 的ε闭包ε-CLOSURE(I)为：

1. 若 q ∈I ,则 q ∈ε_CLOSURE(I)
2. 若 q∈I,那么从 q 出发经任意条ε弧而能到达的任何状态 q’都属于 ε-CLOSURE(I)

定义 2：状态集 I 的 a 转换（状态集 I 经过输入 a 的转换状态集合）

若 I={S1,…,Sm}是 NFA 的状态集的一个子集，对于任意的输入 a∈$∑$，则状态集 I 经过输入 a 转换的状态集合

Ia = ε_CLOSURE(J)

其中: J = f(S1,a) $\cup$ f(S2,a) … $\cup$ f(Sm,a)

算法

已知 A：NFA, 构造 A’:DFA

1. 令 A’的初始状态为 I0’=ε_CLOSURE({S1,S2,…Sk}),其中 S1…Sk 是 A 的全部初始状态。
2. 若 I={S1,…,Sm}是 A’的一个状态，a∈∑，则定义 f’(I, a)=Ia，将 Ia 加入 S’，重复该过程，直到 S’不产生新状态。
3. 若 I’={S1,…,Sn}是 A’的一个状态,且存在一个 Si 是 A 的终止状态，则令 I’为 A’的终止状态。

例子

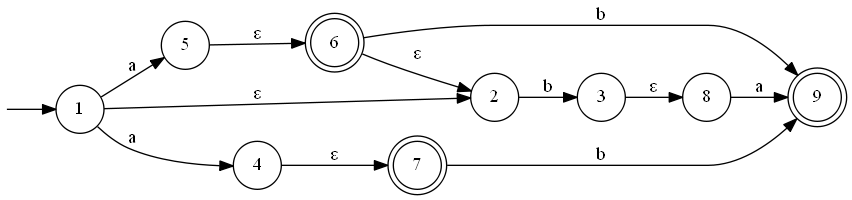
过程如下：

• NFA 的初始状态是 1，该状态可以接收一个空闭包ε到状态 2。因此 DFA 的初始状态是 {1,2}
• 由上可知 DFA 的初始状态是 {1,2}，{1,2} 中的 1 接收输入字 a 可转换到 {4,5}，而 {4,5} 接收空闭包到状态 {6,7}，其中 6 还可以接收空闭包到状态 2。而 2 不能接收输入字 a。因此 {1,2} 接收输入字 a 可转换到 {2,4,5,6,7}。
• {1,2} 中的 1 不能接收输入字 b；2 接收输入字 b 到 状态 3，状态 3 还可以接收空闭包到状态 8。因此 {1,2} 接收输入字 b 到状态 {3,8}。
• 进行如上三步后，DFA 中的状态有 {1,2}、{2,4,5,6,7}、{3,8}，其中 {1,2} 状态转换后的状态已经算完。
• 接下来，我们再看 DFA 的状态 {2,4,5,6,7}。该状态不能接收输入字 a；该状态中的 2 状态接收 b 到达 3 状态，该 3 状态接收空闭包还可到达 8 状态。其中的 6 状态和 7 状态均可接收输入字 b 到达 9 状态。于是 DFA 的状态中多了一个状态{3,8,9}。
• 我们再看 DFA 中状态{3,8}。其中的状态 8 接收输入字 a 可以到达状态 9；状态{3,8}不能接收输入字 b。因此 DFA 的状态增加一个状态 {9}。
• 再来看状态{3,8,9}，其中的状态 8 接收输入字 a 可以到达状态 9；该状态不能接收输入字 b。由于 DFA 中已经有状态{9}，不再重复加入 DFA 的状态。
• 最后只有一个状态 {9} 了，该状态不能接收任何输入字。
• 总结出 DFA 中有状态 {1,2}，{2,4,5,6,7}，{3,8}，{3,8,9}，{9}。其中包含有 NFA 的终止状态 6 7 9 中任意一个状态的状态是 DFA 的终止状态。

制表结果：

状态 \ 输入字	a	b
+{1,2}	{2,4,5,6,7}	{3,8}
-{2,4,5,6,7}	{}	{3,8,9}
{3,8}	{9}	{}
-{3,8,9}	{9}	{}
-{9}	{}	{}

+ - 分别是起始状态和终止状态。

转换后的结果如图所示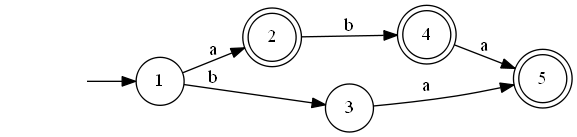

• {1, 2} 对应 1
• {2, 4, 5, 6, 7} 对应 2
• {3, 8} 对应 3
• {3, 8, 9} 对应 4
• {9} 对应 5

参考资料

Nondeterministic finite automaton（这里有提 Nondeterministic finite automaton with ε-moves (NFA-ε) is a further generalization to NFA. ）

《编译原理及实践》

Footnotes

¹ 这个情形非常类似于我们程序中结构化的问题，所谓的结构程序设计有三种结构： 顺序 分支 循环 。特殊的还有一个函数调用。按照这样的结构构造的程序称作是 结构化的程序 。归纳起来就是三种结构，按照这种结构最后可以把程序图归成一个节点，那就非常类似于我们给出的顺序分支循环。但是实际的程序中可能有非结构的情形，例如 goto 语句。那样的程序图就会变的很乱。那就跟我们这里很像，假如 dfa 是结构化的，按照这样的一些规则把他变换过去一点问题都没有，但是大家想假如自动机中有若干的环路套在一起，那用这样几种规则来变换，就不能直接的变换成这种形式，那就需要有一个结构的到非结构的转换，那个就比较复杂了，有所谓的 结构定理 等等，在自动机里也有一些相关的复杂的算法，可以自己看书