- FLOATING-POINT REPRESENTATION
- 在线转化
本文译自 《计算机科学基础-–—从数据操纵到计算理论》
今天因为要用到浮点数怎么转化为二进制进而在计算机里表示,只隐隐约约记得有个 IEEE 什么的,网上的资料也是鱼龙混杂,干脆找到大一的这本书来看看。不看不知道,一看吓一跳。老外写的东西就是简单详细。特此记录。
ps. 这里的 0 1 位有点多,我敲下来难免有错漏,欢迎大家指正。
FLOATING-POINT REPRESENTATION
为了表示一个浮点数(一个有整数部分和小数部分的数)。这个数被分为两部分:整数部分和小数部分。比如,浮点数 14.234 分为 整数部分 14 和 小数部分 0.234.
转化为二进制(CONVERTING TO BINARY)
为了将一个浮点数转化为二进制,我们使用如下步骤:
- 将整数部分转化为二进制
- 将小数部分转化为二进制
- 在两部分之间放一个小数点(put a decimal point between the two parts)
转化整数部分 (Converting the Interger Part)
见第二章。
转化小数部分 (Converting the Fraction Part)
为了将小数转化为二进制,使用连续的乘法。比如,将 0.125 转化为二进制。
- 使用 2 乘这个小数,结果是 0.250。 结果的整数部分(0)被提取出来,作为二进制最左边的那一位。
- 然后继续用 2 乘这个小数部分 (0.250),得到 0.50 结果的整数部分(0)被提取出来,作为下一个二进制位。
- 持续这个过程直到小数部分为 0 或者达到一定精度。
ps. 书上算上这个有三个例子,这里只举一个。
例子
将小数 0.4 转化为 6 位二进制数。
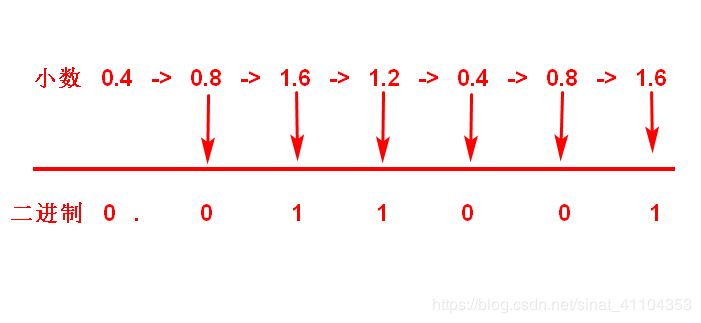
归一化(NORMALIZATION)
为了表示 71.3125(+1000111.0101),我们需要在内存中存上符号、所有比特位和小数点的位置。虽然这个可以实现,但是这将数的操作弄得复杂了。你需要一个浮点数的标准表示形式。解决方法就是 归一化 。归一化就是移动十进制点使得这个点的左边只有一个 1。
为了能够继续表示这个数的原始值,我们需要乘上一个 $2e$。其中 e 就是小数点点移动的位数。然后我们根据原始数的符号添上正负号。
| Original Number | Move | Normalized |
|---|---|---|
| +1010001.11001 | $\gets$ 6 | $+2^6$ × 1.01000111001 |
| -111.000011 | $\gets$ 2 | $-2^2$ × 1.11000011 |
| +0.00000111001 | 6 $\to$ | $+2^{-6}$ × 1.11001 |
| -0.001110011 | 3 $\to$ | $-2^{-3} ×$ × 1.110011 |
符号、指数和尾数(SIGN, EXPONENT, AND MANTISSA)
在一个数被归一化之后,我们只需要存上一个数的部分信息:符号、指数和尾数(小数点右边的比特位)。比如,+1000111.0101 成为
$\space \space \space \space \space \space \space \space \space \space \space \space + \space \space \space \space \space \space \space \space 2^6 \space \space \space\space \space \space\space \space \space\space \space \space\space \space \space\space \space \space\space \space \space × \space \space \space \space \space \space \space 1.0001110101$
$Sign: + \space \space \space \space \space \space \space Exponent:6 \space \space \space \space \space \space \space\space\space \space \space\space \space \space \space Mantissa: 0001110101$
符号(Sign)
数字的符号可以用 1 位来表示。
指数(Exponent)
指数(以 2 为底)定义了小数点移动的距离。注意指数可正可负。指数使用余码表示。分配的位数(N)定义了一个计算机可以存储的数的范围。
尾数(Mantissa)
尾数是指小数点右边的二进制位数。它定义了一个数的精度。尾数被存储为一个无符号整数。
IEEE 标准(IEEE STANDRADS)
IEEE 定义了三种存储浮点数的标准,两种用来表示存储在内存中的数(单精度和双精度)。框框中间的数表示位数。

单精度表示法(Single-Precision Presentation)
在内存中使用单精度格式存储一个归一化过后的浮点数的步骤是:
- 用 0(正数) 或 1(负数) 存储符号
以余127码存储指数(Store the exponent (power of 2) as Excess1271) 博主注:就是给指数加上 127- 使用无符号整数存储尾数(Store the mantissa as an unsigned integer)
例子
| Number | Sign | Exponent | Mantissa |
|---|---|---|---|
| $+2^6$ × 1.01000111001 | 0 | 10000101 | 01000111001000000000000 |
| $-2^2$ × 1.11000011 | 1 | 10000001 | 11000011000000000000000 |
| $+2^{-6}$ × 1.11001 | 0 | 01111001 | 11001000000000000000000 |
| $-2^{-3}$ × 1.110011 | 1 | 01111100 | 11001100000000000000000 |
单精度的浮点数解释(Floating-Point Interpretation for Single Precision)
下面的过程描述了一个 32 位浮点数在内存中的存储情况
- 使用最左边的那位作为符号位
- 把接下来的 8 位转化为十进制,然后减去 127。这部分就是指数
- 在后 23 位前加上
1.。你可以忽略右边多余的 0 - 使用指数值将小数点移动到正确的位置
- 将整部分转化为十进制(Change the whole part to decimal)
- 将小数部分转化为十进制 (Change the fraction part to decimal)
- 将整部分和小数部分合起来(Combine the whole and the fraction parts)
例子
Interpret the following 32-bit floating-point number
\[1\space \space 01111100 \space \space11001100000000000000000\]- 最左边那位是符号(-)
- 接下来 8 位是 01111100。这是十进制的 124。如果你再减去 127,你将得到 指数 -3
- 接下来 23 位是精度。如果你忽略多余的 0,你将得到 110011
- 然后,在你将 1 加到小数点的左边时,归一化后的二进制数是
在线转化
一个在线转换的网址是 http://www.styb.cn/cms/ieee_754.php
Footnotes
1 Excess127 是余 127 码。这部分的知识可以搜索=余码系统=(Excess System),其中的 127 被称为=幻数=(the magic number)。不懂的可以暂时理解 余码 为 移位。